
Precalculus: Mathematics for Calculus (Standalone Book)
7th Edition
ISBN: 9781305071759
Author: James Stewart, Lothar Redlin, Saleem Watson
Publisher: Brooks Cole
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 13.5, Problem 1E
The graph of a function f is shown below.
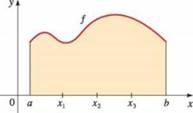
1. To find the area under the graph of f, we first approximate the area by. Approximate the area by drawing four rectangles. The area
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(3) (20 points) Let F(x, y, z) = (y, z, x²z). Define
E = {(x, y, z) | x² + y² ≤ z ≤ 1, x ≤ 0}.
(a) (2 points) Calculate the divergence V. F.
(b) (4 points) Let D = {(x, y) | x² + y² ≤ 1, x ≤ 0} Without calculation, show that
the triple integral
√ (V · F) dV = √ 2²(1.
= x²(1 − x² - y²) dA.
E
(2) (22 points) Let F(x, y, z) = (x sin y, cos y, ―xy).
(a) (2 points) Calculate V. F.
(b) (6 points) Given a vector field
is everywhere defined with V
G₁(x, y, z) = *
G2(x, y, z) = −
G3(x, y, z) = 0.
0
0
F(x, y, z) = (F₁(x, y, z), F₂(x, y, z), F(x, y, z)) that
F = 0, let G = (G1, G2, G3) where
F₂(x,
y,
y, t) dt
- √ F³(x, t, 0) dt,
*
F1(x,
y, t) dt,
t) dt - √ F
Calculate G for the vector field F(x, y, z) = (x sin y, cos y, -xy).
Evaluate the following integral over the Region R.
(Answer accurate to 2 decimal places).
√ √(x + y) A
R
R = {(x, y) | 25 < x² + y² ≤ 36, x < 0}
Hint: The integral and Region is defined in rectangular coordinates.
Chapter 13 Solutions
Precalculus: Mathematics for Calculus (Standalone Book)
Ch. 13.1 - When we write limxaf(x)=L then, roughly speaking,...Ch. 13.1 - We write limxaf(x)=L and say that the ______ of...Ch. 13.1 - Prob. 3ECh. 13.1 - Prob. 4ECh. 13.1 - Prob. 5ECh. 13.1 - Prob. 6ECh. 13.1 - Prob. 7ECh. 13.1 - Prob. 8ECh. 13.1 - Prob. 9ECh. 13.1 - Prob. 10E
Ch. 13.1 - Prob. 11ECh. 13.1 - Prob. 12ECh. 13.1 - Prob. 13ECh. 13.1 - Estimating Limits Numerically and Graphically Use...Ch. 13.1 - Prob. 15ECh. 13.1 - Prob. 16ECh. 13.1 - Prob. 17ECh. 13.1 - Limits from a Graph For the function f whose graph...Ch. 13.1 - Limits from a Graph For the function f whose graph...Ch. 13.1 - Limits from a Graph For the function f whose graph...Ch. 13.1 - Prob. 21ECh. 13.1 - Prob. 22ECh. 13.1 - Prob. 23ECh. 13.1 - Estimating Limits Graphically Use a graphing...Ch. 13.1 - Prob. 25ECh. 13.1 - Prob. 26ECh. 13.1 - Prob. 27ECh. 13.1 - Prob. 28ECh. 13.1 - Prob. 29ECh. 13.1 - One-Sided Limits Graph the piecewise-defined...Ch. 13.1 - Prob. 31ECh. 13.1 - Prob. 32ECh. 13.1 - Prob. 33ECh. 13.1 - DISCUSS: Graphing Calculator Pitfalls (a)...Ch. 13.2 - Suppose the following limits exist:...Ch. 13.2 - If f is a polynomial or a rational function and a...Ch. 13.2 - Limits from a Graph The graphs of f and g are...Ch. 13.2 - Prob. 4ECh. 13.2 - Using Limit Laws Evaluate the limit and justify...Ch. 13.2 - Prob. 6ECh. 13.2 - Prob. 7ECh. 13.2 - Prob. 8ECh. 13.2 - Prob. 9ECh. 13.2 - Prob. 10ECh. 13.2 - Prob. 11ECh. 13.2 - Prob. 12ECh. 13.2 - Prob. 13ECh. 13.2 - Prob. 14ECh. 13.2 - Prob. 15ECh. 13.2 - Prob. 16ECh. 13.2 - Prob. 17ECh. 13.2 - Using Limit Laws Evaluate the limit and justify...Ch. 13.2 - Prob. 19ECh. 13.2 - Prob. 20ECh. 13.2 - Prob. 21ECh. 13.2 - Prob. 22ECh. 13.2 - Prob. 23ECh. 13.2 - Prob. 24ECh. 13.2 - Prob. 25ECh. 13.2 - Prob. 26ECh. 13.2 - Prob. 27ECh. 13.2 - Prob. 28ECh. 13.2 - Prob. 29ECh. 13.2 - Prob. 30ECh. 13.2 - Prob. 31ECh. 13.2 - Prob. 32ECh. 13.2 - Prob. 33ECh. 13.2 - Prob. 34ECh. 13.2 - Prob. 35ECh. 13.2 - Prob. 36ECh. 13.2 - Prob. 37ECh. 13.2 - Prob. 38ECh. 13.2 - Prob. 39ECh. 13.2 - Prob. 40ECh. 13.2 - Does the Limit Exist? Find the limit, if it...Ch. 13.2 - Does the Limit Exist? Find the limit, if it...Ch. 13.2 - Does the Limit Exist? Let f(x)={x1ifx2x24x+6ifx2...Ch. 13.2 - Prob. 44ECh. 13.2 - Finding Limits Numerically and Graphically (a)...Ch. 13.2 - Prob. 46ECh. 13.2 - Prob. 47ECh. 13.2 - Prob. 48ECh. 13.2 - DISCUSS PROVE: Limits of Sums and Products (a)...Ch. 13.3 - The derivative of a function f at a number a is...Ch. 13.3 - Prob. 2ECh. 13.3 - Prob. 3ECh. 13.3 - Prob. 4ECh. 13.3 - Prob. 5ECh. 13.3 - Prob. 6ECh. 13.3 - Prob. 7ECh. 13.3 - Prob. 8ECh. 13.3 - Prob. 9ECh. 13.3 - Prob. 10ECh. 13.3 - Prob. 11ECh. 13.3 - Prob. 12ECh. 13.3 - Equation of a Tangent Line Find an equation of the...Ch. 13.3 - Prob. 14ECh. 13.3 - Prob. 15ECh. 13.3 - Prob. 16ECh. 13.3 - Prob. 17ECh. 13.3 - Prob. 18ECh. 13.3 - Prob. 19ECh. 13.3 - Prob. 20ECh. 13.3 - Prob. 21ECh. 13.3 - Prob. 22ECh. 13.3 - Prob. 23ECh. 13.3 - Prob. 24ECh. 13.3 - Prob. 25ECh. 13.3 - Prob. 26ECh. 13.3 - Prob. 27ECh. 13.3 - Prob. 28ECh. 13.3 - Prob. 29ECh. 13.3 - Prob. 30ECh. 13.3 - Prob. 31ECh. 13.3 - Tangent Lines (a) If g(x) = 1/(2x 1), find g(a)....Ch. 13.3 - Prob. 33ECh. 13.3 - Prob. 34ECh. 13.3 - Prob. 35ECh. 13.3 - Prob. 36ECh. 13.3 - Velocity of a Ball If a ball is thrown straight up...Ch. 13.3 - Velocity on the Moon If an arrow is shot upward on...Ch. 13.3 - Prob. 39ECh. 13.3 - Inflating a Balloon A spherical balloon is being...Ch. 13.3 - Temperature Change A roast turkey is taken from an...Ch. 13.3 - Heart Rate A cardiac monitor is used to measure...Ch. 13.3 - Prob. 43ECh. 13.3 - World Population Growth The table gives...Ch. 13.3 - Prob. 45ECh. 13.3 - Prob. 46ECh. 13.4 - Let f be a function defined on some interval (a,...Ch. 13.4 - Prob. 2ECh. 13.4 - Limits from a Graph (a) Use the graph of f to find...Ch. 13.4 - Prob. 4ECh. 13.4 - Prob. 5ECh. 13.4 - Prob. 6ECh. 13.4 - Prob. 7ECh. 13.4 - Prob. 8ECh. 13.4 - Prob. 9ECh. 13.4 - Prob. 10ECh. 13.4 - Prob. 11ECh. 13.4 - Prob. 12ECh. 13.4 - Prob. 13ECh. 13.4 - Prob. 14ECh. 13.4 - Prob. 15ECh. 13.4 - Prob. 16ECh. 13.4 - Limits at Infinity Find the limit. 17. limxcosxCh. 13.4 - Prob. 18ECh. 13.4 - Prob. 19ECh. 13.4 - Prob. 20ECh. 13.4 - Estimating Limits Numerically and Graphically Use...Ch. 13.4 - Prob. 22ECh. 13.4 - Prob. 23ECh. 13.4 - Prob. 24ECh. 13.4 - Prob. 25ECh. 13.4 - Prob. 26ECh. 13.4 - Prob. 27ECh. 13.4 - Prob. 28ECh. 13.4 - Prob. 29ECh. 13.4 - Prob. 30ECh. 13.4 - Prob. 31ECh. 13.4 - Prob. 32ECh. 13.4 - Prob. 33ECh. 13.4 - Prob. 34ECh. 13.4 - Prob. 35ECh. 13.4 - Prob. 36ECh. 13.4 - Prob. 37ECh. 13.4 - Prob. 38ECh. 13.4 - Salt Concentration (a) A tank contains 5000 L of...Ch. 13.4 - Velocity of a Raindrop The downward velocity of a...Ch. 13.4 - DISCUSS: The Limit of a Recursive Sequence (a) A...Ch. 13.5 - The graph of a function f is shown below. 1. To...Ch. 13.5 - Prob. 2ECh. 13.5 - Estimating an Area Using Rectangles (a) By reading...Ch. 13.5 - Prob. 4ECh. 13.5 - Prob. 5ECh. 13.5 - Prob. 6ECh. 13.5 - Prob. 7ECh. 13.5 - Prob. 8ECh. 13.5 - Prob. 9ECh. 13.5 - Estimating Areas Using Rectangles In these...Ch. 13.5 - Prob. 11ECh. 13.5 - Prob. 12ECh. 13.5 - Prob. 13ECh. 13.5 - Prob. 14ECh. 13.5 - Prob. 15ECh. 13.5 - Prob. 16ECh. 13.5 - Prob. 17ECh. 13.5 - Prob. 18ECh. 13.5 - Prob. 19ECh. 13.5 - Prob. 20ECh. 13.5 - Prob. 21ECh. 13.5 - Prob. 22ECh. 13 - (a) Explain what is meant by limxa f(x) = L. (b)...Ch. 13 - To evaluate the limit of a function, we often need...Ch. 13 - (a) Explain what it means to...Ch. 13 - (a) Define the derivative f(a) of a function f at...Ch. 13 - (a) Give two different interpretations of the...Ch. 13 - (a) Explain what is meant by limx f(x) = L. Draw...Ch. 13 - (a) If a1, a2, a3, is a sequence, what is meant...Ch. 13 - (a) Suppose S is the region under the graph of the...Ch. 13 - Estimating Limits Numerically and Graphically Use...Ch. 13 - Estimating Limits Numerically and Graphically Use...Ch. 13 - Estimating Limits Numerically and Graphically Use...Ch. 13 - Estimating Limits Numerically and Graphically Use...Ch. 13 - Estimating Limits Numerically and Graphically Use...Ch. 13 - Estimating Limits Numerically and Graphically Use...Ch. 13 - Limits from a Graph The graph of f is shown in the...Ch. 13 - One-Sided Limits Let f(x)={2ifx1x2if1x2x+2ifx2...Ch. 13 - Finding Limits Evaluate the limit, if it exists....Ch. 13 - Finding Limits Evaluate the limit, if it exists....Ch. 13 - Finding Limits Evaluate the limit, if it exists....Ch. 13 - Finding Limits Evaluate the limit, if it exists....Ch. 13 - Prob. 13RECh. 13 - Prob. 14RECh. 13 - Prob. 15RECh. 13 - Prob. 16RECh. 13 - Prob. 17RECh. 13 - Prob. 18RECh. 13 - Prob. 19RECh. 13 - Prob. 20RECh. 13 - Prob. 21RECh. 13 - Derivative of a Function Find the derivative of...Ch. 13 - Prob. 23RECh. 13 - Prob. 24RECh. 13 - Prob. 25RECh. 13 - Prob. 26RECh. 13 - Prob. 27RECh. 13 - Prob. 28RECh. 13 - Prob. 29RECh. 13 - Prob. 30RECh. 13 - Prob. 31RECh. 13 - Prob. 32RECh. 13 - Prob. 33RECh. 13 - Prob. 34RECh. 13 - Prob. 35RECh. 13 - Prob. 36RECh. 13 - Prob. 37RECh. 13 - Prob. 38RECh. 13 - Prob. 39RECh. 13 - Prob. 40RECh. 13 - Prob. 41RECh. 13 - Prob. 42RECh. 13 - Prob. 43RECh. 13 - Prob. 44RECh. 13 - Prob. 45RECh. 13 - Prob. 46RECh. 13 - Prob. 47RECh. 13 - Prob. 48RECh. 13 - Prob. 1TCh. 13 - For the piecewise-defined function f whose graph...Ch. 13 - Prob. 3TCh. 13 - Prob. 4TCh. 13 - Prob. 5TCh. 13 - Prob. 6TCh. 13 - Prob. 7TCh. 13 - Work Done by a Winch A motorized winch is being...Ch. 13 - Prob. 2PCh. 13 - Prob. 3PCh. 13 - Prob. 4PCh. 13 - Prob. 5P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Find the volume of the solid that lies under the paraboloid z = 81 - x² - y² and within the cylinder (x − 1)² + y² = 1. A plot of an example of a similar solid is shown below. (Answer accurate to 2 decimal places). Volume using Double Integral Paraboloid & Cylinder -3 Hint: The integral and region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √4(1–2² 4(1 - x² - y²) dA R 3 R = {(r,0) | 0 ≤ r≤ 2,0π ≤0≤¼˜}. Hint: The integral is defined in rectangular coordinates. The Region is defined in polar coordinates.arrow_forwardEvaluate the following integral over the Region R. (Answer accurate to 2 decimal places). R - 1 · {(r,0) | 1 ≤ r≤ 5,½π≤ 0<1π}. Hint: Be sure to convert to Polar coordinates. Use the correct differential for Polar Coordinates.arrow_forward
- Evaluate the following integral over the Region R. (Answer accurate to 2 decimal places). √ √2(x+y) dA R R = {(x, y) | 4 < x² + y² < 25,0 < x} Hint: The integral and Region is defined in rectangular coordinates.arrow_forwardHW: The frame shown in the figure is pinned at A and C. Use moment distribution method, with and without modifications, to draw NFD, SFD, and BMD. B I I 40 kN/m A 3 m 4 marrow_forwardLet the region R be the area enclosed by the function f(x)= = 3x² and g(x) = 4x. If the region R is the base of a solid such that each cross section perpendicular to the x-axis is an isosceles right triangle with a leg in the region R, find the volume of the solid. You may use a calculator and round to the nearest thousandth. y 11 10 9 00 8 7 9 5 4 3 2 1 -1 -1 x 1 2arrow_forward
- Let the region R be the area enclosed by the function f(x) = ex — 1, the horizontal line y = -4 and the vertical lines x = 0 and x = 3. Find the volume of the solid generated when the region R is revolved about the line y = -4. You may use a calculator and round to the nearest thousandth. 20 15 10 5 y I I I | I + -1.5 -1 -0.5 0.5 1 1.5 2 2.5 3 -5 I -10 -15 I + I I T I I + -20 I + -25 I I I -30 I 3.5 4 xarrow_forwardplease show all the workarrow_forwardplease show all the workarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,  Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage


Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill

Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Area Between The Curve Problem No 1 - Applications Of Definite Integration - Diploma Maths II; Author: Ekeeda;https://www.youtube.com/watch?v=q3ZU0GnGaxA;License: Standard YouTube License, CC-BY