In Exercises 1 and 2, create a graph with the given properties. 1. Create a graph with four even vertices, two odd vertices, a bridge, and a loop.

Question

Want to see more full solutions like this?

Answer 1

Textbook Question

Chapter 13, Problem 1RE

In Exercises 1 and 2, create a graph with the given properties.

1. Create a graph with four even vertices, two odd vertices, a bridge, and a loop.

Expert Solution & Answer

To determine

To sketch: A graph with four even vertices, two odd vertices, a bridge and a loop.

Explanation of Solution

One of the possible graph with four even vertices, two odd vertices, a bridge and a loop is shown below in Figure 1.

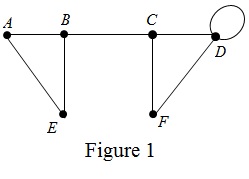
A Survey of Mathematics with Applications (10th Edition) - Standalone book, Chapter 13, Problem 1RE

From Figure 1, it can be observed that the graph has only six vertices and eight edges.

Here the vertices A, E, F, D are even vertices and the vertices B and C are odd vertices.

That is, there are four even vertices and two odd vertices.

Recall that, a bridge is an edge if it is removed from the graph then graph will becomes disconnected.

If the edge BC is removed, the graph will becomes disconnected.

Therefore, BC is a bridge of the graph; also it is the only one bridge of this graph.

Also the graph has a loop at the vertex D.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

Calculus lll May I please have the blank lines completed, and final statement defined as a result? Thank you for the support!

For each month of the year, Taylor collected the average high temperatures in Jackson, Mississippi. He used the data to create the histogram shown. Which set of data did he use to create the histogram? A 55, 60, 64, 72, 73, 75, 77, 81, 83, 91, 91, 92\ 55,\ 60,\ 64,\ 72,\ 73,\ 75,\ 77,\ 81,\ 83,\ 91,\ 91,\ 92 55, 60, 64, 72, 73, 75, 77, 81, 83, 91, 91, 92 B 55, 57, 60, 65, 70, 71, 78, 79, 85, 86, 88, 91\ 55,\ 57,\ 60,\ 65,\ 70,\ 71,\ 78,\ 79,\ 85,\ 86,\ 88,\ 91 55, 57, 60, 65, 70, 71, 78, 79, 85, 86, 88, 91 C 55, 60, 63, 64, 65, 71, 83, 87, 88, 88, 89, 93\ 55,\ 60,\ 63,\ 64,\ 65,\ 71,\ 83,\ 87,\ 88,\ 88,\ 89,\ 93 55, 60, 63, 64, 65, 71, 83, 87, 88, 88, 89, 93 D 55, 58, 60, 66, 68, 75, 77, 82, 86, 89, 91, 91\ 55,\ 58,\ 60,\ 66,\ 68,\ 75,\ 77,\ 82,\ 86,\ 89,\ 91,\ 91 55, 58, 60, 66, 68, 75, 77, 82, 86, 89, 91, 91

In this problem, we consider a Brownian motion (W+) t≥0. We consider a stock model (St)t>0 given (under the measure P) by d.St 0.03 St dt + 0.2 St dwt, with So 2. We assume that the interest rate is r = 0.06. The purpose of this problem is to price an option on this stock (which we name cubic put). This option is European-type, with maturity 3 months (i.e. T = 0.25 years), and payoff given by F = (8-5)+ (a) Write the Stochastic Differential Equation satisfied by (St) under the risk-neutral measure Q. (You don't need to prove it, simply give the answer.) (b) Give the price of a regular European put on (St) with maturity 3 months and strike K = 2. (c) Let X = S. Find the Stochastic Differential Equation satisfied by the process (Xt) under the measure Q. (d) Find an explicit expression for X₁ = S3 under measure Q. (e) Using the results above, find the price of the cubic put option mentioned above. (f) Is the price in (e) the same as in question (b)? (Explain why.)

Answer 2

Textbook Question

Chapter 13, Problem 1RE

In Exercises 1 and 2, create a graph with the given properties.

1. Create a graph with four even vertices, two odd vertices, a bridge, and a loop.

Expert Solution & Answer

To determine

To sketch: A graph with four even vertices, two odd vertices, a bridge and a loop.

Explanation of Solution

One of the possible graph with four even vertices, two odd vertices, a bridge and a loop is shown below in Figure 1.

A Survey of Mathematics with Applications (10th Edition) - Standalone book, Chapter 13, Problem 1RE

From Figure 1, it can be observed that the graph has only six vertices and eight edges.

Here the vertices A, E, F, D are even vertices and the vertices B and C are odd vertices.

That is, there are four even vertices and two odd vertices.

Recall that, a bridge is an edge if it is removed from the graph then graph will becomes disconnected.

If the edge BC is removed, the graph will becomes disconnected.

Therefore, BC is a bridge of the graph; also it is the only one bridge of this graph.

Also the graph has a loop at the vertex D.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Answer 3

Textbook Question

Chapter 13, Problem 1RE

In Exercises 1 and 2, create a graph with the given properties.

1. Create a graph with four even vertices, two odd vertices, a bridge, and a loop.

Expert Solution & Answer

To determine

To sketch: A graph with four even vertices, two odd vertices, a bridge and a loop.

Explanation of Solution

One of the possible graph with four even vertices, two odd vertices, a bridge and a loop is shown below in Figure 1.

A Survey of Mathematics with Applications (10th Edition) - Standalone book, Chapter 13, Problem 1RE

From Figure 1, it can be observed that the graph has only six vertices and eight edges.

Here the vertices A, E, F, D are even vertices and the vertices B and C are odd vertices.

That is, there are four even vertices and two odd vertices.

Recall that, a bridge is an edge if it is removed from the graph then graph will becomes disconnected.

If the edge BC is removed, the graph will becomes disconnected.

Therefore, BC is a bridge of the graph; also it is the only one bridge of this graph.

Also the graph has a loop at the vertex D.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Answer 4

Textbook Question

Chapter 13, Problem 1RE

In Exercises 1 and 2, create a graph with the given properties.

1. Create a graph with four even vertices, two odd vertices, a bridge, and a loop.

Expert Solution & Answer

To determine

To sketch: A graph with four even vertices, two odd vertices, a bridge and a loop.

Explanation of Solution

One of the possible graph with four even vertices, two odd vertices, a bridge and a loop is shown below in Figure 1.

A Survey of Mathematics with Applications (10th Edition) - Standalone book, Chapter 13, Problem 1RE

From Figure 1, it can be observed that the graph has only six vertices and eight edges.

Here the vertices A, E, F, D are even vertices and the vertices B and C are odd vertices.

That is, there are four even vertices and two odd vertices.

Recall that, a bridge is an edge if it is removed from the graph then graph will becomes disconnected.

If the edge BC is removed, the graph will becomes disconnected.

Therefore, BC is a bridge of the graph; also it is the only one bridge of this graph.

Also the graph has a loop at the vertex D.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Answer 5

Textbook Question

Answer 6

Textbook Question

Answer 7

Expert Solution & Answer

To determine

To sketch: A graph with four even vertices, two odd vertices, a bridge and a loop.

Explanation of Solution

One of the possible graph with four even vertices, two odd vertices, a bridge and a loop is shown below in Figure 1.

A Survey of Mathematics with Applications (10th Edition) - Standalone book, Chapter 13, Problem 1RE

From Figure 1, it can be observed that the graph has only six vertices and eight edges.

Here the vertices A, E, F, D are even vertices and the vertices B and C are odd vertices.

That is, there are four even vertices and two odd vertices.

Recall that, a bridge is an edge if it is removed from the graph then graph will becomes disconnected.

If the edge BC is removed, the graph will becomes disconnected.

Therefore, BC is a bridge of the graph; also it is the only one bridge of this graph.

Also the graph has a loop at the vertex D.

Answer 8

Expert Solution & Answer

To determine

To sketch: A graph with four even vertices, two odd vertices, a bridge and a loop.

Explanation of Solution

One of the possible graph with four even vertices, two odd vertices, a bridge and a loop is shown below in Figure 1.

A Survey of Mathematics with Applications (10th Edition) - Standalone book, Chapter 13, Problem 1RE

From Figure 1, it can be observed that the graph has only six vertices and eight edges.

Here the vertices A, E, F, D are even vertices and the vertices B and C are odd vertices.

That is, there are four even vertices and two odd vertices.

Recall that, a bridge is an edge if it is removed from the graph then graph will becomes disconnected.

If the edge BC is removed, the graph will becomes disconnected.

Therefore, BC is a bridge of the graph; also it is the only one bridge of this graph.

Also the graph has a loop at the vertex D.

Answer 9

Expert Solution & Answer

Answer 10

Expert Solution & Answer

Answer 11

To determine

To sketch: A graph with four even vertices, two odd vertices, a bridge and a loop.

Answer 12

Explanation of Solution

One of the possible graph with four even vertices, two odd vertices, a bridge and a loop is shown below in Figure 1.

A Survey of Mathematics with Applications (10th Edition) - Standalone book, Chapter 13, Problem 1RE

From Figure 1, it can be observed that the graph has only six vertices and eight edges.

Here the vertices A, E, F, D are even vertices and the vertices B and C are odd vertices.

That is, there are four even vertices and two odd vertices.

Recall that, a bridge is an edge if it is removed from the graph then graph will becomes disconnected.

If the edge BC is removed, the graph will becomes disconnected.

Therefore, BC is a bridge of the graph; also it is the only one bridge of this graph.

Also the graph has a loop at the vertex D.

Answer 13

Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - Prob. 5E Ch. 13.1 - In Exercises 1-8, fill in the blanks with an...Ch. 13.1 - Prob. 7E Ch. 13.1 - Prob. 8E Ch. 13.1 - In Exercises 9-14, create a graph with the given...Ch. 13.1 - In Exercises 9-14, create a graph with the given...

In Exercises 1 and 2, create a graph with the given properties. 1. Create a graph with four even vertices, two odd vertices, a bridge, and a loop.

Videos

Explanation of Solution

Want to see more full solutions like this?

Chapter 13 Solutions