
Concept explainers
Often, we model the Moon as a particle in a circular orbit around the Earth. The same side of the Moon always faces the Earth. Sketch the Moon in its orbit. Explain in what way the particle model is insufficient.
Sketch the Moon’s orbit. Explain why the particle model is insufficient.
Answer to Problem 1PQ
The orbit of moon is sketched below
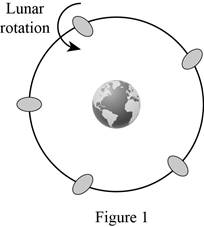
Particle model is insufficient in explaining the orbital motion of moon, because rotating object cannot be modeled as a simple particle in translational motion.
Explanation of Solution
Orbital motion of Moon is shown below.
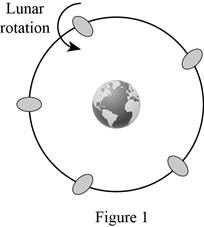
The motion of moon around sun is a best example of circular motion. Moon revolving around Earth in such a way that keeping same side always facing Earth, and revolves in its on axis.
During the rotation of moon earth also spins in its axis. A rotating object cannot be considered as simple particle in translational motion. Thus particle model is insufficient to represent a motion as shown in figure 1.
Want to see more full solutions like this?
Chapter 12 Solutions
Physics for Scientists and Engineers: Foundations and Connections
- A 70.0 cm, uniform, 40.0 N shelf is supported horizontally by two vertical wires attached to the sloping ceiling (Figure 1). A very small 20.0 N tool is placed on the shelf midway between the points where the wires are attached to it. Find the tension in the left-hand wire. Express your answer with the appropriate units.arrow_forwardFind the total bind Mev. binding energy for 13 Carbon, 6C (atomic mass = 13.0033554)arrow_forwardWhat is the 27 energy absorbed in this endothermic Auclear reaction 2] Al + 'n → 27 Mg + ! H? (The atom mass of "Al is 26.981539u. and that of 11 Mg is 26.984341u) MeVarrow_forward
- What is the energy released in this nuclear reaction 1 F + "', H-1 O+ He? 19 19 16 (The atomic mass of 1F is 18.998403 u, and that of 20 is 15.9949154) MeV.arrow_forwardWhat is the energy released in this B+ nuclear reaction خالد 2½ Al w/ Mg + ie? (The atomic mass of 11 Al is 23.9999394 and that > of 12 Mg is 23.985041 u) MeV.arrow_forwardWhat is the energy released / absorbed in this nuclear reaction 14 N+ & He → » O + ! N? (The atomic mass of 14 N is 14.003074u. 17N+ and that of 10 is 16.9991324). MeVarrow_forward
- Can someone help me answer this question thanks.arrow_forwardCan someone help me with this question thanks.arrow_forward4B. Four electrons are located on the corners of a square, one on each corner, with the sides of the square being 25 cm long. a) Draw a sketch of the scenario and use your sketch to b) Determine the total force (magnitude and direction) on one of the electrons from the other three?arrow_forward
- Portfolio Problem 3. A ball is thrown vertically upwards with a speed vo from the floor of a room of height h. It hits the ceiling and then returns to the floor, from which it rebounds, managing just to hit the ceiling a second time. Assume that the coefficient of restitution between the ball and the floor, e, is equal to that between the ball and the ceiling. Compute e.arrow_forwardPortfolio Problem 4. Consider two identical springs, each with natural length and spring constant k, attached to a horizontal frame at distance 2l apart. Their free ends are attached to the same particle of mass m, which is hanging under gravity. Let z denote the vertical displacement of the particle from the hori- zontal frame, so that z < 0 when the particle is below the frame, as shown in the figure. The particle has zero horizontal velocity, so that the motion is one dimensional along z. 000000 0 eeeeee (a) Show that the total force acting on the particle is X F-mg k-2kz 1 (1. l k. (b) Find the potential energy U(x, y, z) of the system such that U x = : 0. = O when (c) The particle is pulled down until the springs are each of length 3l, and then released. Find the velocity of the particle when it crosses z = 0.arrow_forwardIn the figure below, a semicircular conductor of radius R = 0.260 m is rotated about the axis AC at a constant rate of 130 rev/min. A uniform magnetic field of magnitude 1.22 T fills the entire region below the axis and is directed out of the page. R Pout (a) Calculate the maximum value of the emf induced between the ends of the conductor. 1.77 v (b) What is the value of the average induced emf for each complete rotation? 0 v (c) How would your answers to parts (a) and (b) change if the magnetic field were allowed to extend a distance R above the axis of rotation? (Select all that apply.) The value in part (a) would increase. The value in part (a) would remain the same. The value in part (a) would decrease. The value in part (b) would increase. The value in part (b) would remain the same. The value in part (b) would decrease. × (d) Sketch the emf versus time when the field is as drawn in the figure. Choose File No file chosen This answer has not been graded yet. (e) Sketch the emf…arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





