
In
a. The reflection with axis
b. The reflection with axis
c. The reflection with axis
d. The reflection with axis
1.
To find:
The image of
Answer to Problem 1E
Solution:
The image of point P under the reflection with axis
Explanation of Solution
Given:
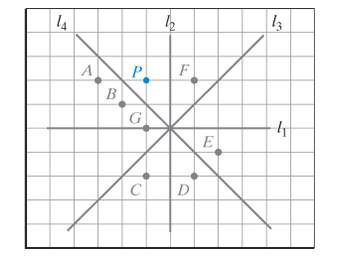
The given figure is,
A rigid motion that moves the object from its starting position to a new position, namely the mirror image of the starting position is called a reflection in the plane.
If a point
To find a image of point
Consider the given figure,
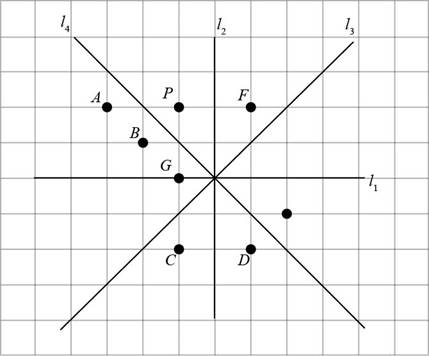
Figure (1)
In the given figure, the points E, C, and D lie on the opposite side of
Points E, D are opposite to point P but do not have same distance from
The point C is at same distance from
The image of P is point C.
Conclusion:
Thus, the image of point P under the reflection with axis
(b)
To find:
The image of
Answer to Problem 1E
Solution:
The image of point P under the reflection with axis
Explanation of Solution
Given:
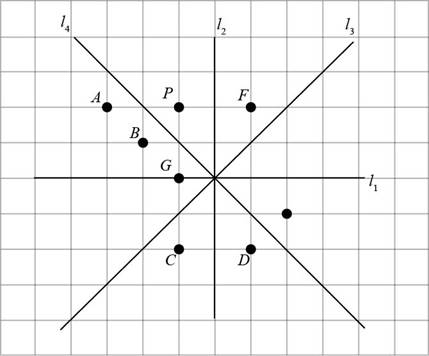
The given figure is,
A rigid motion that moves the object from its starting position to a new position, namely the mirror image of the starting position is called a reflection in the plane.
If a point
To find a image of point
Consider the given figure,
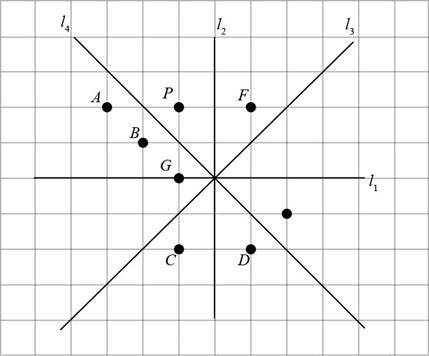
Figure (2)
In Figure (1), the points E, F, and D lie on the opposite side of
Points E, D are opposite to point P but do not have same distance from
The point F is at same distance from
The image of P is point F.
Conclusion:
Thus, the image of point P under the reflection with axis
(c)
To find:
The image of
Answer to Problem 1E
Solution:
The image of
Explanation of Solution
Given:
The given figure is,

A rigid motion that moves the object from its starting position to a new position, namely the mirror image of the starting position is called a reflection in the plane.
If a point
To find a image of point
Consider the given figure,

Figure (3)
In the given figure, the points C, D, and E lie on the opposite side of
Points C and D are opposite to point P but do not have same distance from
Point E has same distance from
The image of P is point E.
Conclusion:
Thus, the image of point P under the reflection with axis
(d)
To find:
The image of
Answer to Problem 1E
Solution:
The image of
Explanation of Solution
Given:
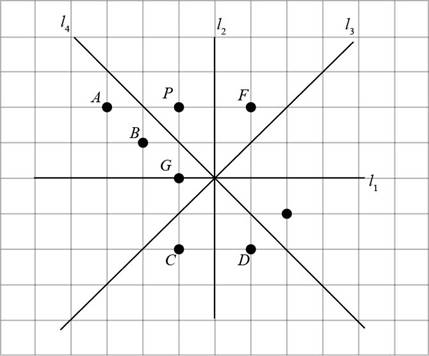
The given figure is,
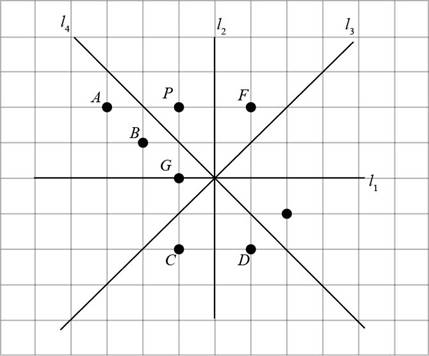
A rigid motion that moves the object from its starting position to a new position, namely the mirror image of the starting position is called a reflection in the plane.
If a point
To find a image of point
Consider the given figure,

Figure (4)
In the given figure, the points A, B, C, D, and G lie on the opposite side of
Points A, D, C and G are opposite to point P but do not have same distance from
Distance of point B from
The image of P is point B.
Conclusion:
Thus, the image of point P under the reflection with axis
Want to see more full solutions like this?
Chapter 11 Solutions
Excursions in Modern Mathematics (9th Edition)
Additional Math Textbook Solutions
Precalculus: A Unit Circle Approach (3rd Edition)
Pathways To Math Literacy (looseleaf)
Elementary & Intermediate Algebra
College Algebra (Collegiate Math)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
- A company estimates that the revenue (in dollars) from the sale of x doghouses is given by R(x) = 12,000 In (0.02x+1). Use the differential to approximate the change in revenue from the sale of one more doghouse if 80 doghouses have already been sold. The revenue will increase by $ if one more doghouse is made. (Round to the nearest cent as needed.)arrow_forwardThe population of bacteria (in millions) in a certain culture x hours after an experimental 20x nutrient is introduced into the culture is P(x) = - 2 Use the differential to approximate the changes in population for the following changes in x. 8+x a. 1 to 1.5 b. 3 to 3.25 a. Use the differential to approximate the change in population for x=1 to 1.5. Between 1 and 1.5 hours, the population of bacteria changes by million. (Round to three decimal places as needed.)arrow_forwardThe demand for grass seed (in thousands of pounds) at price p dollars is given by the following function. D(p) 3p³-2p² + 1460 Use the differential to approximate the changes in demand for the following changes in p. a. $4 to $4.11 b. $6 to $6.19arrow_forward
- Let the region R be the area enclosed by the function f(x) = 3 ln (x) and g(x) = 3 x + 1. Write an integral in terms of x and also an integral in terms of y that would represent the area of the region R. If necessary, round limit values to the nearest thousandth. Answer Attempt 1 out of 2 y 7 10 6 5 4 3 2 -1 2 3 4 5 6 x2 dx x1 = x2 = x1 Y1 = Y2 = Y1 dyarrow_forwardA manufacturer of handcrafted wine racks has determined that the cost to produce x units per month is given by C = 0.3x² + 7,000. How fast is the cost per month changing when production is changing at the rate of 14 units per month and the production level is 80 units? Costs are increasing at the rate of $ (Round to the nearest dollar as needed.) per month at this production level.arrow_forwarddy Assume x and y are functions of t. Evaluate for 2xy -3x+2y³ = - 72, with the conditions dt dx dt = -8, x=2, y = -3. dy dt (Type an exact answer in simplified form.)arrow_forward
- Discuss and explain in the picturearrow_forwardConsider the cones K = = {(x1, x2, x3) | € R³ : X3 ≥√√√2x² + 3x² M = = {(21,22,23) (x1, x2, x3) Є R³: x3 > + 2 3 Prove that M = K*. Hint: Adapt the proof from the lecture notes for finding the dual of the Lorentz cone. Alternatively, prove the formula (AL)* = (AT)-¹L*, for any cone LC R³ and any 3 × 3 nonsingular matrix A with real entries, where AL = {Ax = R³ : x € L}, and apply it to the 3-dimensional Lorentz cone with an appropriately chosen matrix A.arrow_forwardI am unable to solve part b.arrow_forward
- Consider the sequence below: 1 1 1 (a) Express this sequence as a recurrence relation (b) Express this sequence in the form {a}=1 (c) Does this sequence converge or diverge? Justify your answer. Consider the sequence below: 1 1 1 1, 4' 9' 16' (a) Express this sequence in the form {ak}=1 (b) Does this sequence converge or diverge? Justify your answer. Consider the sequence below: 345 2. 4' 9' 16' ·} (a) Express this sequence in the form {a}1 (b) Does this sequence converge or diverge? Justify your answer.arrow_forwardLet M = M₁U M₂ UM3 and K M₁ = {(x1, x2) ER²: 2 ≤ x ≤ 8, 2≤ x ≤8}, M₂ = {(x1, x2)™ € R² : 4 ≤ x₁ ≤ 6, 0 ≤ x2 ≤ 10}, M3 = {(x1, x2) Є R²: 0 ≤ x₁ ≤ 10, 4≤ x ≤ 6}, ¯ = cone {(1, 2), (1,3)†} ≤ R². (a) Determine the set E(M,K) of efficient points of M with respect to K. (b) Determine the set P(M, K) of properly efficient points of M with respect to K.arrow_forward5.17 An aluminum curtain wall panel 12 feet high is attached to large concrete columns (top and bottom) when the temperature is 65°F. No provision is made for differen- tial thermal movement vertically. Because of insulation between them, the sun heats up the wall panel to 120°F but the column to only 80°F. Determine the consequent compressive stress in the curtain wall. CONCRETE COLUMNS CONNECTIONS Stress= ALUMINUM WALL PANEL 12'-0"arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL  Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell




