
Concept explainers
In Problems 1-4, find all critical points and determine whether they are relative
To calculate: The critical values, relative maxima, relative minima, or horizontal points of inflection of the function
Answer to Problem 1RE
Solution:
The critical value(s) are
Explanation of Solution
Given Information:
The provided equation is
Formula Used:
The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.
This, in an interval between two critical values, the sign of the derivative at any value in the interval will be the sign of the derivative at all values in the interval.
As per the First Derivative Test,
The first derivative of the function is evaluated. The first derivative is made equal to zero in order to get the critical points.
The values of the critical values are kept inside the original function which gives the critical points. The intervals of the values of x are then evaluated for the relative maximum and minimum.
Calculation:
Consider the provided equation
The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.
Hence, there will no change in the values of critical values as in the derivative graph.
Take out the first derivative of the equation by the power rule,
Put the value of
Hence, the values of x are
Evaluate the values of the original functions with the critical values:
Put
Hence,
The relative maximum can be evaluated as follows by two ways, it can be understood as reaching a peak after increasing, and then going for a downfall.
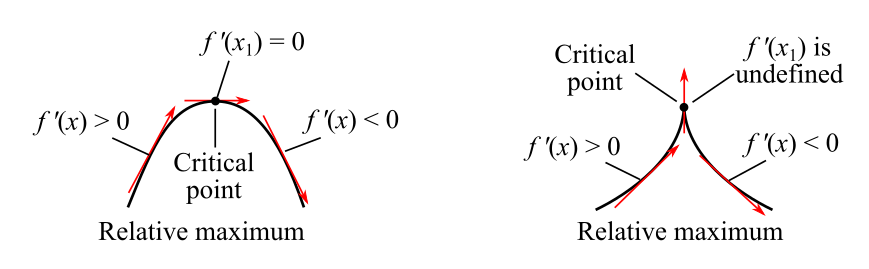
It can be observed that there is
The relative minimum can be evaluated as follows by two ways, it can be understood as reaching a peak after decreasing, and then going upward.
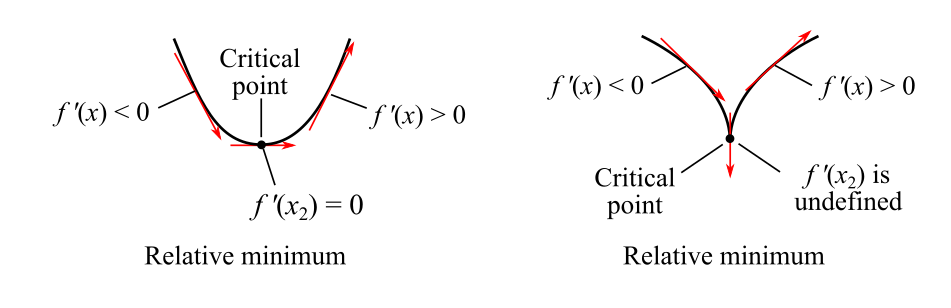
It can be observed that there is no relative minima.
If the first derivative of f is 0 at
In this case, it is said that f has a horizontal point of inflection.
The horizontal point of inflection is not there.
Want to see more full solutions like this?
Chapter 10 Solutions
Mathematical Applications for the Management, Life, and Social Sciences
- Use the spinner shown to answer the question. Assume that it is equally probable that the pointer will land on any one of the colored regions. If the pointer lands on a borderline, spin again. If the spinner is spun once, find the probability that the pointer lands in a region that is red or green. The probability that the pointer lands in a region that is red or green is (Type an integer or a simplified fraction.) green red green red yellow redarrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forwardA survey of 250 young professionals found that two-thirds of them use their cell phones primarily for e-mail. Can you conclude statistically that the population proportion who use cell phones primarily for e-mail is less than 0.72? Use a 95% confidence interval. Question content area bottom Part 1 The 95% confidence interval is [ ], [ ] As 0.72 is ▼ above the upper limit within the limits below the lower limit of the confidence interval, we ▼ can cannot conclude that the population proportion is less than 0.72. (Use ascending order. Round to four decimal places as needed.)arrow_forward
- 2. Answer the following questions using vectors u and v. --0-0-0 = find the the cosine similarity and the angle between u and v. འརྒྱ (a) (b) find the scalar projection of u onto v. (c) find the projection of u onto v. (d) (e) (f) find the scalar projection of onto u. find the projection of u onto u. find the projection of u onto and the projection of onto . (Hint: find the inner product and verify the orthogonality)arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forward
- I need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forwardLet $f(x)$ be a continuous function on the interval $[0,1]$ such that $f(0) = f(1) = 0$. Prove that for any positive integer $n$, there exists a real number $x$ in $[0, 1 - \frac{1}{n}]$ such that $f(x) = f(x + \frac{1}{n})$.arrow_forwardK/FT イ 5 SLOPE AB TB3.3 C 15 TROY 16.7 y Yo 13.3 GIVEN: BEAM + LOADING DRAW V+H SOLUTION: DIAGRAMS 1) FIND REACTIONS R=14/15 (20) = 20k (@EMB=20F (5) - Roy(15) RRY = 6.7k EFу=0= 20+67+RBY RBY = 13.3k+ 5 6.7 roarrow_forward
- Pls help ASAParrow_forward9. a) Determie values of a and b so that the function is continuous. ax - 2b f(x) 2 x≤-2 -2x+a, x ≥2 \-ax² - bx + 1, −2 < x < 2) 9b) Consider f(x): = 2x²+x-3 x-b and determine all the values of b such that f(x) does not have a vertical asymptote. Show work.arrow_forwardPls help ASAParrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill




