
Concept explainers
In Problems 1-4, find all critical points and determine whether they are relative
To calculate: The critical values, relative maxima, relative minima, or horizontal points of inflection of the function
Answer to Problem 1RE
Solution:
The critical value(s) are
Explanation of Solution
Given Information:
The provided equation is
Formula Used:
The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.
This, in an interval between two critical values, the sign of the derivative at any value in the interval will be the sign of the derivative at all values in the interval.
As per the First Derivative Test,
The first derivative of the function is evaluated. The first derivative is made equal to zero in order to get the critical points.
The values of the critical values are kept inside the original function which gives the critical points. The intervals of the values of x are then evaluated for the relative maximum and minimum.
Calculation:
Consider the provided equation
The critical values are the only values at which the graph can have turning points, the derivative cannot change sign anywhere except at the critical value.
Hence, there will no change in the values of critical values as in the derivative graph.
Take out the first derivative of the equation by the power rule,
Put the value of
Hence, the values of x are
Evaluate the values of the original functions with the critical values:
Put
Hence,
The relative maximum can be evaluated as follows by two ways, it can be understood as reaching a peak after increasing, and then going for a downfall.
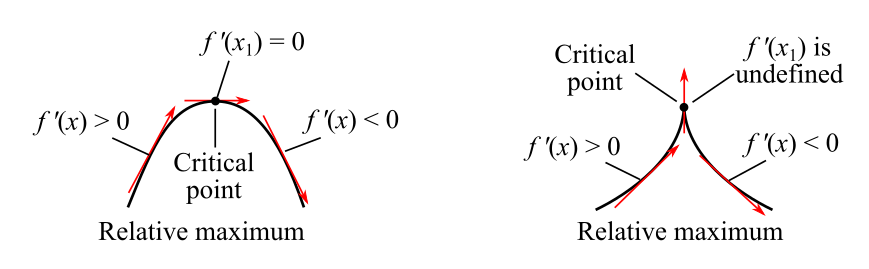
It can be observed that there is
The relative minimum can be evaluated as follows by two ways, it can be understood as reaching a peak after decreasing, and then going upward.
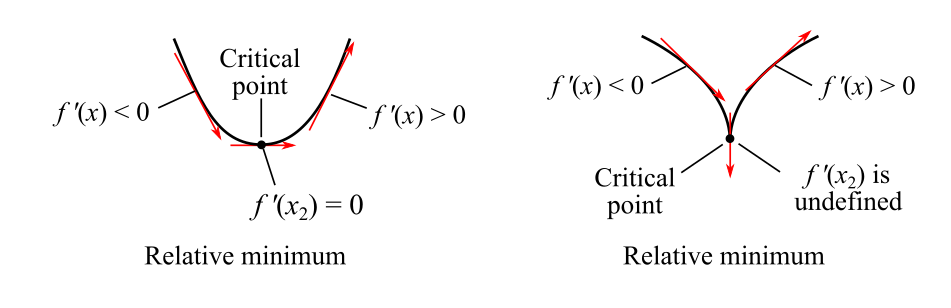
It can be observed that there is no relative minima.
If the first derivative of f is 0 at
In this case, it is said that f has a horizontal point of inflection.
The horizontal point of inflection is not there.
Want to see more full solutions like this?
Chapter 10 Solutions
Mathematical Applications for the Management, Life, and Social Sciences
- ५ (x² + 2x-y³) (16 x + 15) dy (x+2+y2) (x+2)3 =arrow_forward(28 points) Define T: [0,1] × [−,0] → R3 by T(y, 0) = (cos 0, y, sin 0). Let S be the half-cylinder surface traced out by T. (a) (4 points) Calculate the normal field for S determined by T.arrow_forwardQuestion 21 of 28 (1 point) | Question Attempt: 5 of Unlimited Dorothy ✔ ✓ 12 ✓ 13 ✓ 14 ✓ 15 ✓ 16 ✓ 17 ✓ 18 ✓ 19 ✓ 20 = 21 22 > How many apps? According to a website, the mean number of apps on a smartphone in the United States is 82. Assume the number of apps is normally distributed with mean 82 and standard deviation 30. Part 1 of 2 (a) What proportion of phones have more than 47 apps? Round the answer to four decimal places. The proportion of phones that have more than 47 apps is 0.8783 Part: 1/2 Try again kip Part ی E Recheck == == @ W D 80 F3 151 E R C レ Q FA 975 % T B F5 10 の 000 园 Save For Later Submit Assignment © 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Center | Accessibility Y V& U H J N * 8 M I K O V F10 P = F11 F12 . darrow_forward
- (14 points) Let S = {(x, y, z) | z = e−(x²+y²), x² + y² ≤ 1}. The surface is the graph of ze(+2) sitting over the unit disk. = (a) (4 points) What is the boundary OS? Explain briefly. (b) (4 points) Let F(x, y, z) = (e³+2 - 2y, xe³±² + y, e²+y). Calculate the curl V × F.arrow_forward(6 points) Let S be the surface z = 1 − x² - y², x² + y² ≤1. The boundary OS of S is the unit circle x² + y² = 1. Let F(x, y, z) = (x², y², z²). Use the Stokes' Theorem to calculate the line integral Hint: First calculate V x F. Jos F F.ds.arrow_forwardQ5. Manager of car dealership is trying to see how number of sale associates can affect number of final sales in his dealership. He collects the following information: Number of cars Number of working sale associates per day sold in one day 2 2 3 5 3 3 4 1 3 1 2 4 5 Calculate the correlation coefficient for this data set using the equation given on slide#77? Comment on the association of the two variables. ΣΥ) - Σ) × Σ(Υ) (X) E(Y) N 2 (Σ(x²) - 2x²) × (Σ(12) - ²) N Narrow_forward
- You are provided with data that includes all 50 states of the United States. Your task is to draw a sample of: 20 States using Random Sampling (2 points: 1 for random number generation; 1 for random sample) 10 States using Systematic Sampling (4 points: 1 for random numbers generation; 1 for generating random sample different from the previous answer; 1 for correct K value calculation table; 1 for correct sample drawn by using systematic sampling) (For systematic sampling, do not use the original data directly. Instead, first randomize the data, and then use the randomized dataset to draw your sample. Furthermore, do not use the random list previously generated, instead, generate a new random sample for this part. For more details, please see the snapshot provided at the end.) You are provided with data that includes all 50 states of the United States. Your task is to draw a sample of: o 20 States using Random Sampling (2 points: 1 for random number generation; 1 for random sample) o…arrow_forward(28 points) Define T: [0,1] × [−,0] → R3 by T(y, 0) = (cos 0, y, sin 0). Let S be the half-cylinder surface traced out by T. (a) (4 points) Calculate the normal field for S determined by T.arrow_forwardDungeons and Dragons: Part A A 20-sided die is often used in tabletop role-playing games like Dungeons and Dragons. During the game players may face something called a "skill check" where they must roll a 20-sided die and get a result equal to or above a given value. For example, a player may be required to roll a 15 or above in order to succeed and pass the skill check. Rolling a 14 or lower would be a failure. If the player rolls the die 10 times in a row, what is the expected number of rolls that would pass the skill check by rolling as a 15 or higher? For the previous calculations, what is the standard deviation for the number of times the die would be rolled 15 or above During a game of Dungeons and Dragons, the previously-mentioned player rolls the 20-sided die 30 times in total. What is the probablity that they successfully roll a 15 or higher exactly 7 times during that game? Express your final answer as a percentage to 2 decimal places.arrow_forward
- Q3. The distribution for the working lifetime of light bulbs, manufactured in a company, is found to be normally distributed with a mean of 1450 hours and a standard deviation of 60 hours. a) In this distribution, find the life time of a lightbulb whose z-score is -1.8? b) Which percentage of lightbulbs have life time less than 1400 hours? c) Which percentage of lightbulbs have life time greater than 1500 hours? d) Which percentage of lightbulbs have life time between 1420 to 1500 hours?arrow_forwardQ4. Considering the following two normal distributions A and B, which statement (or statements) is correct? a) Mode of the distribution A is larger than that of distribution B. b) SD of the distribution B is larger than that of distribution A. c) Mean of the distribution A is smaller than that of distribution B. d) A data item with z-score of -1 falls between 20 to 30 in distribution A. e) A data item with z-score of +1 falls between 10 to 20 in distribution B. A 0 10 20 30 40 40 50 60 00 10 70 B 80 90 100arrow_forwardQ1. A traffic camera recorded number of red cars going through the intersection at 16th Ave N and Centre St. each day over 7 days was: 32 30 24 30 36 38 27 a) Calculate the mean, mode, range and median of the data set above. c) Calculate the standard deviation of this data set. Sarrow_forward
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill




