Chapter 10, Problem 1RE

In Problems 1 and 2, is the matrix game strictly determined?

$\left[\begin{array}{cc}5& -3\\ -4& 2\end{array}\right]$

To determine

Whether the matrix game $\left[\begin{array}{cc}5& -3\\ -4& -2\end{array}\right]$ is strictly determined or not.

Answer to Problem 1RE

The matrix game $\left[\begin{array}{cc}5& -3\\ -4& -2\end{array}\right]$ is not strictly determined.

Explanation of Solution

Consider the following matrix game.

$\left[\begin{array}{cc}5& -3\\ -4& -2\end{array}\right]$

Now, a saddle value is a payoff value which is both a row minimum and a column maximum of a payoff matrix.

Locate the saddle values.

Circle the minimum value in each row.

So, the matrix game will become,

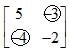
Place squares around the maximum payoff in each column of the matrix game.

In matrix game, none of the payoffs is both row minimum and column maximum.

So, the matrix game does not have a saddle value.

If the matrix game has a saddle value, then it is said to be strictly determined.

Hence, the matrix game is not strictly determined.