
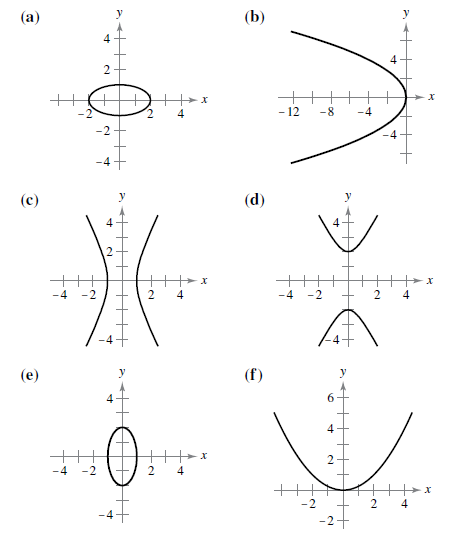
Matching In Exercises 1-6, match the equation with its graph. [The graphs are labeled (a), (b), (c), (d), (e), and (f).]
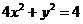
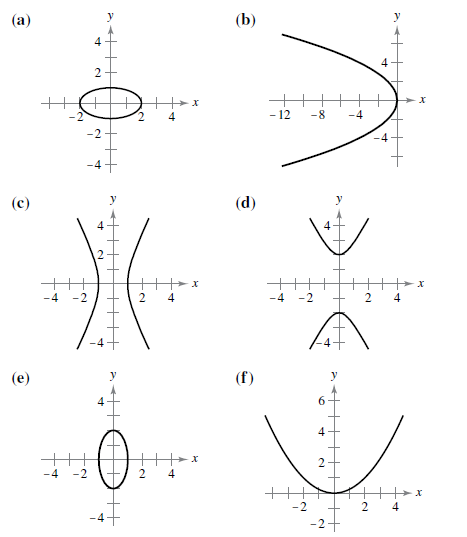
If the equation
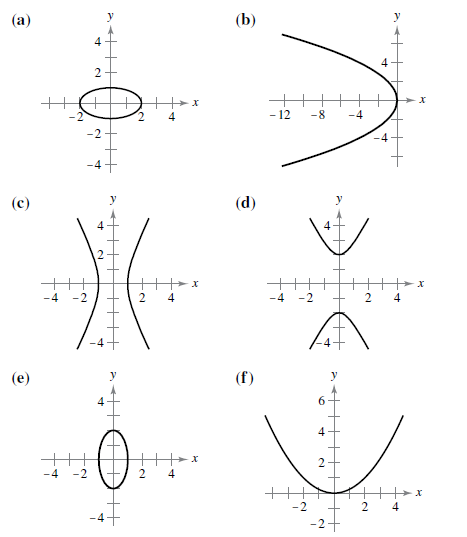
Answer to Problem 1RE
Solution:
The equation
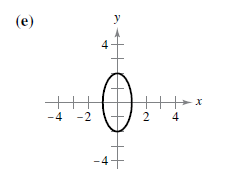
Explanation of Solution
Given:
The options are:
Explanation:
Here,
Now, in order to find whether the ellipse is horizontal or vertical, represent the equation in the standard form of an ellipse.
The given equation is:
Divide the equation by
Rearrange it in standard form as:
So,
Which is the standard equation for an ellipse, whose major axis is vertical. That is the center of ellipse is
Thus, the correct graph matches for the equation that holds the above properties is option (e).
Want to see more full solutions like this?
Chapter 10 Solutions
Calculus of a Single Variable
Additional Math Textbook Solutions
APPLIED STAT.IN BUS.+ECONOMICS
Elementary Statistics (13th Edition)
Elementary Statistics
Precalculus
Precalculus: A Unit Circle Approach (3rd Edition)
Elementary & Intermediate Algebra
- i don't understand how to get these answers please help!arrow_forwardEnter your answer in interval notation. No decimal entries allowed. Type oo (lower case o) for ∞ and -oo for -∞ if needed. Domain: Question Help: Message instructorarrow_forwardWrite a formula for the function g that results when the graph of the function f(x) = = 4 X is reflected about the y-axis, horizontally compressed by a factor of 2, shifted 7 units left, reflected about the x-axis and shifted 3 units up. g(x): = Question Help: Message instructorarrow_forward
- Question 7 4 pts 1 Details The value of China's exports of automobiles and parts (in billions of dollars) is approximately f(x) = 1.8208e0.3387x, where x = 0 corresponds to 1998. In what year did/will the exports reach $10.4 billion?arrow_forwardQuestion 7 4 pts 1 Detai The value of China's exports of automobiles and parts (in billions of dollars) is approximately f(x) = 1.8208e 0.3387x, where x = 0 corresponds to 1998. In what year did/will the exports reach $10.4 billion?arrow_forwardWrite a formula for the function g that results when the graph of the function f(x) = = 4 X is reflected about the y-axis, horizontally compressed by a factor of 2, shifted 7 units left, reflected about the x-axis and shifted 3 units up. g(x) = Question Help: Message instructorarrow_forward
- Question 3 Use the graph of f to evaluate the following: 3 pts 1 D 6 f(x) 5 4 3 2 1 -1 1 2 3 4 5 เค -1 x The average rate of change of f from 1 to 4 =arrow_forwardB Find the domain the function graphed below. Express in interval notation 5 3 pts 1 De 3 2 1 -5 -4 -3 2 -1 2 3 4 5 -2 -3 -4 5 Domain:arrow_forwardFind the domain the function graphed below. Express in interval notation 3 2 -5 4-3 12 -1 1 2 3 4 2 -3- 4 5+ Domain: Question Help: Message instructor Question 3arrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning





