Find f'(x) and simplify. x + 6 x² f(x) = Which of the following shows the correct application of the quotient rule? O A. O B. O C. 9x - 2 O D. (x² +6) (9) - (9x-2)(2x) [9x - 21² (9x − 2)(2x) − (x² + 6) (9) [x² +6]² (x² + 6) (9) − (9x − 2)(2x) [x²+6]² 2 (9x-2)(2x) - (x²+6) (9) [9x-2]²
Find f'(x) and simplify. x + 6 x² f(x) = Which of the following shows the correct application of the quotient rule? O A. O B. O C. 9x - 2 O D. (x² +6) (9) - (9x-2)(2x) [9x - 21² (9x − 2)(2x) − (x² + 6) (9) [x² +6]² (x² + 6) (9) − (9x − 2)(2x) [x²+6]² 2 (9x-2)(2x) - (x²+6) (9) [9x-2]²
Algebra and Trigonometry (6th Edition)
6th Edition
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:Robert F. Blitzer
ChapterP: Prerequisites: Fundamental Concepts Of Algebra
Section: Chapter Questions
Problem 1MCCP: In Exercises 1-25, simplify the given expression or perform the indicated operation (and simplify,...
Related questions
Question
![The task is to find the derivative of the function \( f(x) = \frac{x^2 + 6}{9x - 2} \) using the quotient rule and simplify the result. The quotient rule states that for a function \( \frac{u}{v} \), the derivative is given by:
\[
f'(x) = \frac{v \cdot u' - u \cdot v'}{v^2}
\]
In this problem, four options are provided to determine which one correctly applies the quotient rule.
### Options:
**A.**
\[
\frac{(x^2 + 6)(9) - (9x - 2)(2x)}{[9x - 2]^2}
\]
**B.**
\[
\frac{(9x - 2)(2x) - (x^2 + 6)(9)}{[x^2 + 6]^2}
\]
**C.**
\[
\frac{(x^2 + 6)(9) - (9x - 2)(2x)}{[x^2 + 6]^2}
\]
**D.**
\[
\frac{(9x - 2)(2x) - (x^2 + 6)(9)}{[9x - 2]^2}
\]
The correct application applies the formula \(\frac{v \cdot u' - u \cdot v'}{v^2}\) using \(u = x^2 + 6\), \(v = 9x - 2\), \(u' = 2x\), and \(v' = 9\).
The correct expression should use \(9x - 2\) for \(v\) in the denominator squared, and the numerator should match the expression derived from differentiating \(u\) and \(v\) appropriately.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F0e03da4d-971c-4230-a070-21ed988e0d0e%2F988adcdc-c0e0-4af9-b9f9-20749eac567f%2Fzk82sk3_processed.png&w=3840&q=75)
Transcribed Image Text:The task is to find the derivative of the function \( f(x) = \frac{x^2 + 6}{9x - 2} \) using the quotient rule and simplify the result. The quotient rule states that for a function \( \frac{u}{v} \), the derivative is given by:
\[
f'(x) = \frac{v \cdot u' - u \cdot v'}{v^2}
\]
In this problem, four options are provided to determine which one correctly applies the quotient rule.
### Options:
**A.**
\[
\frac{(x^2 + 6)(9) - (9x - 2)(2x)}{[9x - 2]^2}
\]
**B.**
\[
\frac{(9x - 2)(2x) - (x^2 + 6)(9)}{[x^2 + 6]^2}
\]
**C.**
\[
\frac{(x^2 + 6)(9) - (9x - 2)(2x)}{[x^2 + 6]^2}
\]
**D.**
\[
\frac{(9x - 2)(2x) - (x^2 + 6)(9)}{[9x - 2]^2}
\]
The correct application applies the formula \(\frac{v \cdot u' - u \cdot v'}{v^2}\) using \(u = x^2 + 6\), \(v = 9x - 2\), \(u' = 2x\), and \(v' = 9\).
The correct expression should use \(9x - 2\) for \(v\) in the denominator squared, and the numerator should match the expression derived from differentiating \(u\) and \(v\) appropriately.
Expert Solution
Step 1
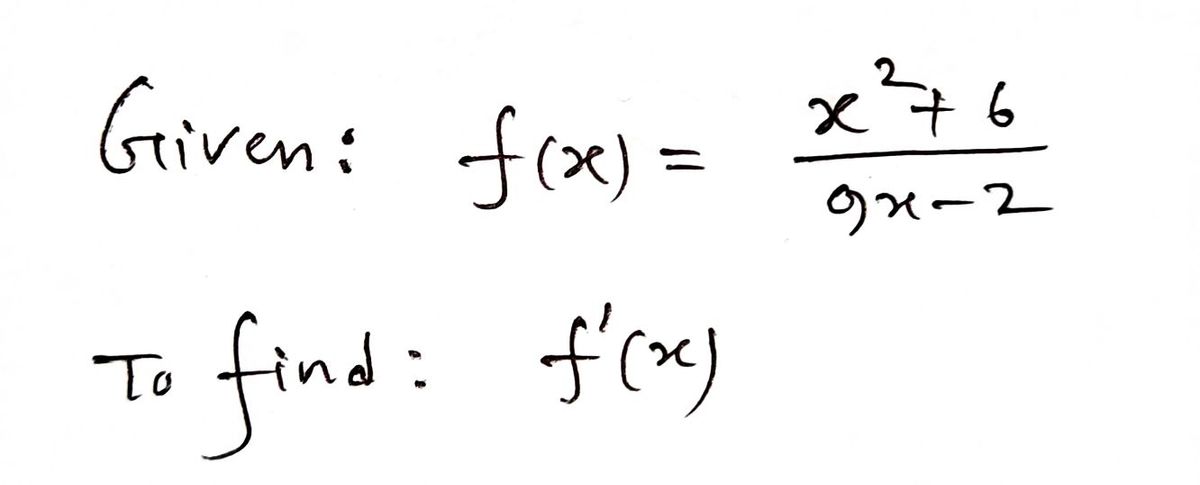
Step by step
Solved in 2 steps with 2 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question
![Find f'(x) and simplify.
x² +
f(x) =
O A.
Which of the following shows the correct application of the quotient rule?
B.
+6
f'(x) =
9x - 2
(x²+6) (9) - (9x-2)(2x)
[9x - 21²
(9x − 2)(2x) − (x² + 6) (9)
[x² +6]²
(x²+6) (9)-(9x-2)(2x)
[x² +6]²
(9x − 2)(2x) − (x² + 6) (9)
[9x-21²](https://content.bartleby.com/qna-images/question/0e03da4d-971c-4230-a070-21ed988e0d0e/dc689526-b58c-4d15-af79-54ba30ec78c1/2o2iaff_thumbnail.png)
Transcribed Image Text:Find f'(x) and simplify.
x² +
f(x) =
O A.
Which of the following shows the correct application of the quotient rule?
B.
+6
f'(x) =
9x - 2
(x²+6) (9) - (9x-2)(2x)
[9x - 21²
(9x − 2)(2x) − (x² + 6) (9)
[x² +6]²
(x²+6) (9)-(9x-2)(2x)
[x² +6]²
(9x − 2)(2x) − (x² + 6) (9)
[9x-21²
Solution
Recommended textbooks for you

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra and Trigonometry (6th Edition)
Algebra
ISBN:
9780134463216
Author:
Robert F. Blitzer
Publisher:
PEARSON

Contemporary Abstract Algebra
Algebra
ISBN:
9781305657960
Author:
Joseph Gallian
Publisher:
Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:
9781285463247
Author:
David Poole
Publisher:
Cengage Learning

Algebra And Trigonometry (11th Edition)
Algebra
ISBN:
9780135163078
Author:
Michael Sullivan
Publisher:
PEARSON

Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:
9780980232776
Author:
Gilbert Strang
Publisher:
Wellesley-Cambridge Press

College Algebra (Collegiate Math)
Algebra
ISBN:
9780077836344
Author:
Julie Miller, Donna Gerken
Publisher:
McGraw-Hill Education