b.A clothing manufacturer makes trousers, skirts and blouses. Each trouser requires 20 minutes of cutting time, 60 minutes of sewing time and 5 minutes of packaging time. Each skirt requires 15 minutes of cutting time, 30 minutes of sewing time and 12 minutes of packaging time. Each blouse requires 10 minutes of cutting time, 24 minutes of sewing time and 6 minutes of packaging time. The amount of time available for cutting, sewing and packaging is 115 hours, 280 hours and 65 hours respectively. Using either the Inverse Method or the Cramer’s Rule, determine how many of each type of clothing should be made to use all available labor hours?
b.A clothing manufacturer makes trousers, skirts and blouses. Each trouser requires 20 minutes of cutting time, 60 minutes of sewing time and 5 minutes of packaging time. Each skirt requires 15 minutes of cutting time, 30 minutes of sewing time and 12 minutes of packaging time. Each blouse requires 10 minutes of cutting time, 24 minutes of sewing time and 6 minutes of packaging time.
The amount of time available for cutting, sewing and packaging is 115 hours, 280 hours and 65 hours respectively. Using either the Inverse Method or the Cramer’s Rule, determine how many of each type of clothing should be made to use all available labor hours?
The following information is given:

Here the inverse method is used to find the number of trousers, skirts, and blouses.
Let P, Q, and R are the numbers of trousers, skirts, and blouses. With the help of table and amount of available time following equations can be written:
Cutting time, 20P + 15Q + 10R = 115 × 60 = 6,900
Sewing time, 60P + 30Q + 24R = 280 × 60 = 16,800
Packaging time, 5P + 12Q + 16R = 65 × 60 = 3,900
Writing these equations in matrix form, the result is:
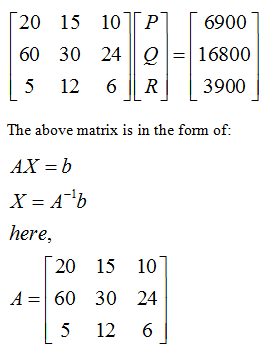
Step by step
Solved in 2 steps with 8 images









